Artigos sobre Fractais:

1. Introdução aos Fractais
2. O Caos e a Ordem - Introdução mitológica
3. Texturas Fractais
4. Padrões Geométricos de Penrose
5. Antigos fractais brasileiros - 1987
6. Livros recomendados - Bibliografia sobre fractais
7. A Matemática do Delírio - Fractais e o Grupo Fractarte na revista "Super Interessante" (matéria da capa)
8. Gráficos 3D com Wolfram Alpha
9. Blog e Álbum de Fotos feito com o Postbit

1. Introdução aos Fractais

"Nuvens não são esferas, montanhas não são cones, continentes não são círculos,
o som do latido não é contínuo e nem o raio viaja em linha reta."
(Benoît Mandelbrot, em seu livro " The Fractal Geometry of Nature " - 1983)

Imagem gerada utilizando fractais através da infinita repetição de padrões similares. Cada pequena parte é similar ao todo.

A ciência dos fractais apresenta estruturas geométricas de grande complexidade e beleza infinita, ligadas às formas da natureza, ao desenvolvimento da vida e à própria compreensão do universo. São imagens de objetos abstratos que possuem o caráter de onipresença por terem as características do todo infinitamente multiplicadas dentro de cada parte, escapando assim, da compreensão em sua totalidade pela mente humana.       Essa geometria, nada convencional, tem raízes remontando ao século XIX e algumas indicações neste sentido vêm de muito antes na Grécia Homérica, Índia, China, entre outros. Porém, somente há poucos anos vem se consolidando com o desenvolvimento dos computadores e o auxílio de novas teorias nas áreas da física, biologia, astronomia e matemática. O termo "fractal" foi criado em 1975 pelo pesquisador Benoît Mandelbrot, o "pai dos fractais".       Diferentes definições de Fractais surgiram com o aprimoramento de sua teoria. A noção que serve de fio condutor foi introduzida por Benoît Mandelbrot através do neologismo "Fractal", que surgiu do adjetivo latino fractus, que significa "irregular" ou "quebrado".

      Uma primeira definição matemática, pelo próprio Mandelbrot, diz: - "Um conjunto é dito Fractal se a dimensão Hausdorff-Besicovitch deste conjunto for maior do que sua dimensão topológica". No decorrer do tempo ficou claro que esta definição era muito restritiva embora tenha motivações pertinentes.

      Uma definição mais simples é esta: "Fractais são objetos gerados pela repetição de um mesmo processo recursivo, apresentando auto-semelhança e complexidade infinita."

Os fractais podem apresentar uma infinidade de formas diferentes, não existindo uma aparência consensual. Contudo, existem duas características muito freqüentes nesta geometria: Complexidade Infinita: É uma propriedade dos fractais que significa que nunca conseguiremos representá-los completamente, pois a quantidade de detalhes é infinita. Sempre existirão reentrâncias e saliências cada vez menores. Auto-similaridade: Um fractal costuma apresentar cópias aproximadas de si mesmo em seu interior. Um pequeno pedaço é similar ao todo. Visto em diferentes escalas a imagem de um fractal parece similar.     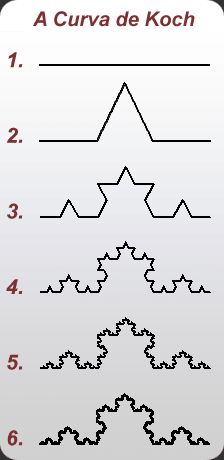A imagem ao lado ("A Curva de Koch") é um exemplo geométrico da construção de um fractal. Um mesmo procedimento é aplicado diversas vezes sobre um objeto simples, gerando uma imagem complexa. Cada pedaço da linha foi dividido em 4 pedaços menores idênticos ao pedaço original, cada um sendo 3 vezes menor que o tamanho original. Assim, usando um novo conceito de dimensão, os matemáticos calcularam a dimensão fractal deste objeto como sendo:     D = log(n.cópias)/log(escala) = log(4)/log(3) = 1,26185.

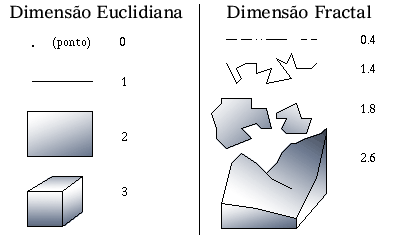
Uma nova geometria e um novo conceito de dimensão precisaram
ser criados para explicar a geometria das formas intrincadas.

      A Geometria Fractal pode ser utilizada para descrever diversos fenômenos na natureza, onde não podem ser utilizadas as geometrias tradicionais. Nuvens, montanhas, turbulências, árvores, crescimento de populações, vasos sangüíneos e outras formas irregulares podem ser estudadas e descritas utilizando as propriedades dos fractais.

Rodrigo Siqueira
Grupo Fractarte
18 de abril de 2005